Figure 2
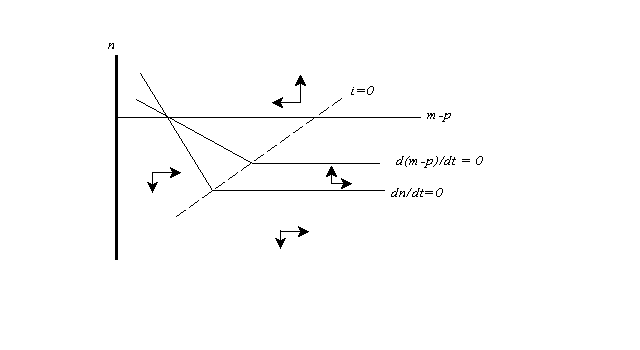
Figure 3
SYNOPSIS: Looks at the growing concensus that Deflation is a possibility. Analyzes mathematical implications.
Among the growing number of observers who now regard deflation as a serious risk for the world's major economies, there is a subtle difference of opinion about the sources of that danger. One view - which is the one that I have espoused for Japan, and set out most recently in my piece Can deflation be prevented? , is that deflationary pressures are essentially structural: the economy's equilibrium real interest rate is negative, and so even with a near-zero nominal interest rate it remains underemployed and generates gradual deflation unless policymakers somehow manage to create expectations of enough inflation to get the real interest rate down where it belongs.
The other view is that while deflation can be a real danger, that danger arises less because of an inherent deflationary bias than as the potential consequence of policy mistakes; the general idea is that once mistaken policies have allowed deflation to get started, expectations of continuing deflation can be self-reinforcing. And once the economy is in such a deflationary "death spiral", the story goes, it can be very hard to get it out again.
These views are not mutually exclusive: one can believe that there are structural forces that give an economy a choice between adequate inflation and grinding deflation - with no middle ground - and also believe that waiting too long to face up to that choice can lead to a downward spiral. But the logic of deflationary spirals implies that even an economy whose equilibrium real interest rate is positive can get into a deflationary trap if its central bankers are too cautious, too preoccupied with fighting the last war. By the time they realize that the nature of the danger has changed, it can be too late. (Any resemblance to current debates about European policy is completely intentional).
In this note I take a standard macroeconomic model, slightly modified by introducing a floor of zero on the nominal interest rate - that is, by introducing the possibility of a liquidity trap - and show that it quite naturally generates both the possibility of a deflationary death spiral and the implication that central bankers may have a window of opportunity in preventing such a spiral that, once missed, is gone for good.
The standard model
Consider a simple, rather old-fashioned IS-LM-type model of an economy in which expectations of inflation are adaptive rather than "rational" - that is, in which people form views about future inflation based on past experience rather than based on considerations of future government policies and so on. I assume that the expected inflation rate that enters into the wage-price process is the same as the expected rate that affects spending decisions; the result is a model similar to that used in standard macroeconomics texts like Dornbusch/Fischer or Gordon. The model considers only a closed economy; as argued in Japan: still trapped an open-economy version would behave in a qualitatively similar way.
For convenience, the model is log-linearized. First, the deviation of real output from its "natural" level depends on the real interest rate:
(1) y = a - b(i - n)
where i is the nominal interest rate, and n the expected rate of inflation.
Next, the demand for real balances depends on income and the nominal interest rate:
(2) m - p = c + dy - ei
The rate of inflation is determined via an expectations-augmented Phillips curve:
(3) dp/dt = hy + n
with expectations of inflation adjusting gradually in response to actual inflation:
(4) dn/dt = k(dp/dt - n)
Finally, monetary policy consists of assigning a constant growth rate to the money supply:
(5) dm/dt = g
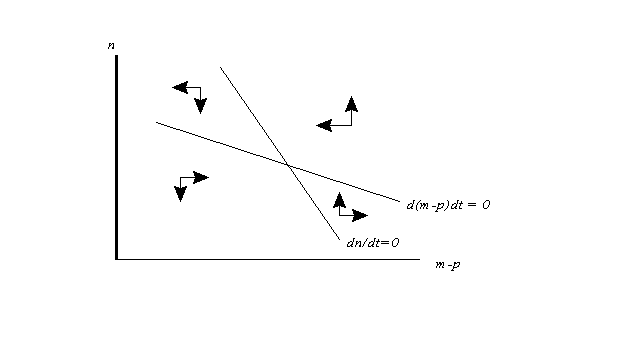
To analyze this model, it is easiest to think of dynamics in the space illustrated in Figure 1 . On the horizontal axis is the real money stock, m-p. On the vertical axis is the expected rate of inflation, n.
Two schedules are shown. One is the locus of points along which y = 0, that is, output is at its natural level, and hence (from (3)) at which the expected rate of inflation does not change. Because expected inflation reduces the real interest rate, and hence expands the economy other things equal, this schedule is downward sloping. The other is the locus of points along which actual inflation equals the rate of money growth, so that the real quantity of money does not change. Since higher expected inflation means higher actual inflation, and so does a larger real money supply, this schedule is also downward-sloping. It is straightforward to show, however, that the second schedule is flatter than the first.
The arrows indicate the dynamics of the system. The system is not self-evidently stable, but if expectations do not adjust too quickly it will be.
The conventional exercise in this model is to consider the effects of a change - say, an increase - in the rate of money growth. Such an increase shifts the schedule d(m-p)/dt = 0 up, and thus leads in the long run to a higher expected inflation rate and smaller real money supply; however, on the way the economy will experience a temporary increase in output followed by a period of "stagflation" as output falls and inflation rises. All this is standard stuff, the staple of intermediate textbooks.
But now let us modify the model slightly, by recognizing that the nominal interest rate cannot be negative, and hence that the money demand function (2) must become perfectly elastic at a zero interest rate.
Adding the liquidity trap
Figure 2 shows what happens to the dynamics when a zero lower bound on the interest rate is introduced. The interest rate itself, of course, depends on the expected rate of inflation and the real money supply - positively on the first, negatively on the second. So we can draw a line (the dotted line in the figure) along which i =0.
When the schedules of Figure 1 cross this line, they make a sharp left turn. That is, the real money supply becomes irrelevant at the margin, and so the schedules become flat, with output and inflation depending only on the expected inflation rate.
I have drawn this figure for the case of a zero rate of increase in the money supply, so that the equilibrium rate of inflation is zero, and have also drawn it so that the zero constraint will not bind at that rate - that is, the equilibrium real interest rate is positive. Nonetheless, the economy can still get into a liquidity trap if people expect sufficiently rapid deflation.
What is immediately apparent is that if the economy gets into the southeastern region of the diagram - below the line y = 0, so that the economy has excess capacity, and also below the line i = 0, so that it is in a liquidity trap - it cannot get out. The output gap feeds expectations of deflation, and since the nominal interest rate cannot fall this implies a rising real interest rate, worsening the output gap. The economy, in short, falls into a deflationary spiral. And once the economy is in such a spiral, accelerating the rate of monetary growth will (if we take the model literally) do nothing to stop it.
We may believe that in practice there may be some natural limits to this process: even in the 1930s the economy eventually found a bottom. But the picture is simple and plausible enough to make concerns about such a "death spiral" entirely reasonable.
A window of opportunity?
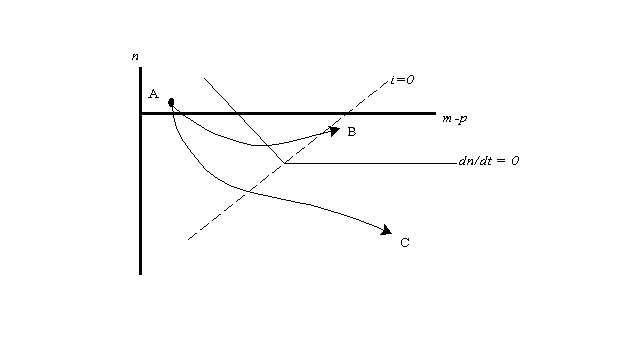
Imagine an economy with "incipient" deflation - that is, prices are either rising slightly or falling slightly, but there is a substantial output gap; so far, however, deflation has not yet gotten built into expectations, and the nominal interest rate is still positive. One might intuitively suspect that in this case there is a window of opportunity for the central bank: if it launches a vigorous monetary expansion immediately, it can still steer the economy away from the deflationary spiral, but if it misses this window, deflation may pass the point of no return.
This intuition is confirmed by the model. Consider Figure 3 , in which only the schedules dn/dt = 0 and i = 0 are shown. The economy is assumed to be initially at point A. Where it goes depends crucially on the near-term rate of money growth. If money growth is rapid, it follows a path like B, avoiding the liquidity trap; but if the central bank is cautious, and waits to see definite evidence of deflation before acting, it will instead follow a path like C, so that by the time the need for a more expansionary policy is unmistakable it is also too late.
This is, of course, only a simple and highly stylized model. But the resemblance to reality is strong enough to be worrisome; conservative monetary policy may seem prudent and responsible to the European Central Bank today, just as it did to the Bank of Japan not long ago, but in retrospect that supposed prudence may look like disastrous folly.